GREEDY ALGORITHM AND ITS APPLICATIONS

Written by:

Fagun Shadi D-53

Tejas Shantaram D-71

Shruti Vasave D-76

Vidhi Raghvani D-77

 The Greedy Property:
                    "make a choice that seems best at the moment then solve sub problems that arise later".

The greedy algorithms are based on this certain property. Greedy algorithms are in fact greedy. 

They're concerned with what the global optimal solution is therein very moment instead of looking into the longer term . This suggests that the general optimal solution could be different from the answer that the algorithm chooses at the start .

This is actually the main difference between greedy strategy and dynamic programming - in dynamic programming, all sub problems are solved, then one among them is chosen to find the optimal solution. Whereas greedy algorithms never optimize globally.

Greedy algorithms can’t always guarantee solutions, but they're very time efficient. We’ll also see later how sometimes greedy strategy solutions do give optimal solutions.

What are greedy algorithms used for ?

As we talked about earlier, greedy algorithms are very time efficient; in order that they are pretty fast in comparison to the opposite alternatives - Divide and conquer or dynamic programming .

Not all, but there are a couple of algorithms that are known to offer globally optimal solutions every time. Let’s have a glance at what these algorithms are.

• Dijkstra’s algorithm
• Kruskal’s algorithm
•  Prim’s algorithm
•  Huffman trees

Let’s explore these greedy algorithms. 

Dijkstra’s algorithm  

This algorithm is especially used to solve any shortest distance problem. For instance, the shortest distance between two points on a graph or shortest routes.

Dijkstra’s algorithm has a lot of uses. They are often very useful within road networks where you would like to seek out the fastest and shortest route to an area .

Other places where this algorithm is used include IP Routing, A*Algorithm, Telephone networks, etc.

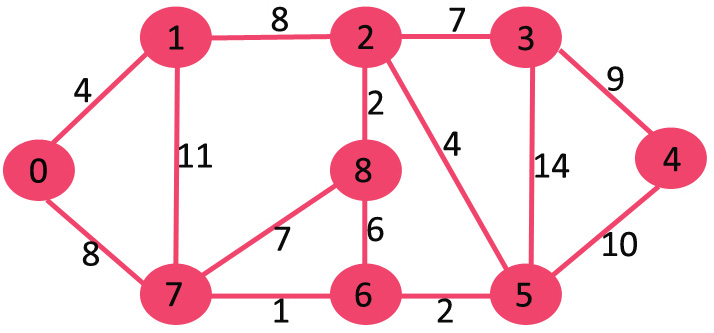Dijkstra's Algorithm

Kruskal’s Algorithm

This algorithm solves the problem of finding a Minimum Spanning Tree (MST) of any connected and undirected graph.

Kruskal’s is a greedy approach that mainly emphasizes on the very fact that we must include only those edges in our MST that have minimum weight among all of them, ensuring that we don't include those edges that make a cycle in MST being constructed.

Kruskal's Algorithm

Prim’s Algorithm

Prim’s algorithm is a slightly different approach than Kruskal’s. It's another greedy algorithm that finds a minimal spanning tree in a connected, weighted graph.

As we see in Kruskal’s, the partial solutions aren't connected usually, but in Prim’s the partial solution is a tree.

The greedy rule applied in Prims algorithm “Add an edge of minimum weight that has one vertex within the current tree and therefore the other not within the current tree.

Prim's Algorithm

Huffman Trees

Huffman Tree is full binary tree in which each leaf of the tree corresponds to a letter within the given alphabet. It's a data compression algorithm which uses the greedy strategy.

The greedy rule applied here is: "at each iteration, the algorithm makes a “greedy” decision to merge the 2 subtrees with least weight."

Huffman Trees